정렬 알고리즘
- 정렬 이란 특정 기준에 따라 데이터 구성~을 의미하다
- 일반적으로 문제 상황에 따라 수식과 같은 적절한 정렬 알고리즘을 사용한다.
- 정렬 알고리즘데이터를 정렬하면 이진 검색이것이 가능해진다(이진 검색의 전처리이기도 하기 때문에 정렬 알고리즘이 중요하다.)
다양한 정렬 알고리즘에 대해 자세히 알아보세요.
정렬 선택
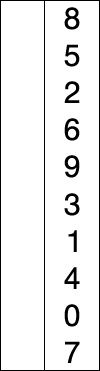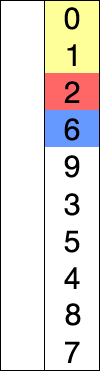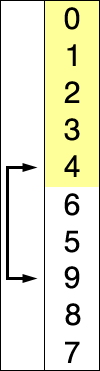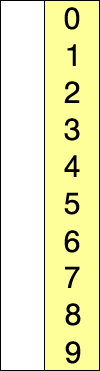
- 선택열 처리되지 않은 데이터 중 가장 작은 데이터를 선택하고 앞의 데이터로 교체를 반복합니다. 하다.
즉, 정렬되지 않은 데이터 중에서 가장 작은 데이터를 선택하여 첫 번째 데이터로 교체한 후 다음으로 작은 데이터를 선택하는 과정을 반복한다.
선택 정렬 알고리즘 코드(Python)
# 선택 정렬을 사용하여 오름차순 정렬
arr = (7, 5, 9, 0, 3, 1, 6, 2, 4, 8)
for i in range(len(arr)):
min_idx = i # 가장 작은 원소의 인덱스
for j in range(i + 1, len(arr)):
if arr(min_idx) > arr(j):
min_idx = j
arr(min_idx), arr(i) = arr(i), arr(min_idx)
print(arr)
>>> (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)- 시간적 복잡성~이다 O(N^2) 오전.
선택 정렬은 가장 작은 숫자를 N번 찾아 앞으로 이동합니다. 또한 구현 방법에 따라 약간의 오류가 있을 수 있으나 총 연산 횟수는 N + (N – 1) + (N – 2) + … + 2 입니다.
이것은 (N^2 + N -2) / 2로 표현할 수 있으며 Big-O 표기법에서는 단순히 O(N^2)입니다.
※ 정렬 선택 은 데이터 개수가 10,000개 이상이면 선택 정렬 속도가 빠르게 느려지는 것을 확인하였다.할수있다.
| 데이터 수(N) | 정렬 선택 | 빠른 종류 | 기본 정렬 라이브러리 |
| N=100 | 0.0123초 | 0.00156초 | 0.00000753초 |
| N=1,000 | 0.354초 | 0.00343초 | 0.0000365초 |
| N=10,000 | 15.475초 | 0.0312초 | 0.000248초 |
측정 시간은 컴퓨터마다 다를 수 있습니다. 상대적인 개념으로 이해합시다.
삽입으로 정렬
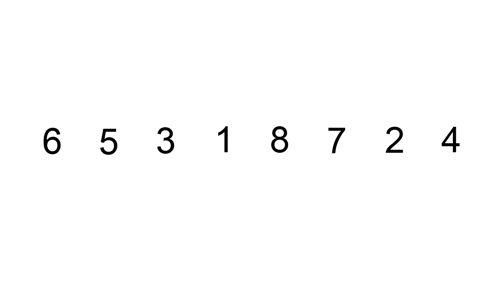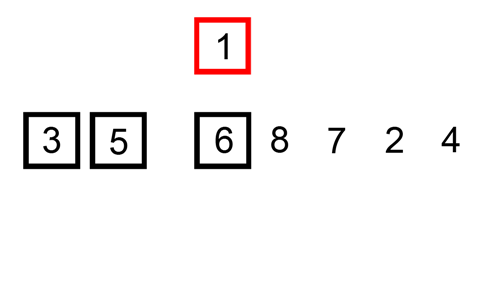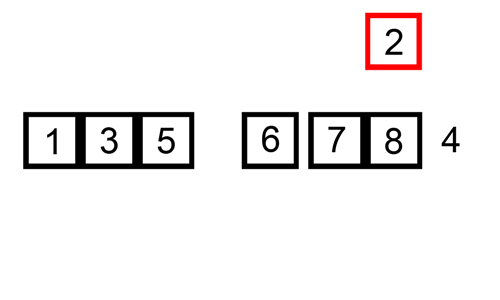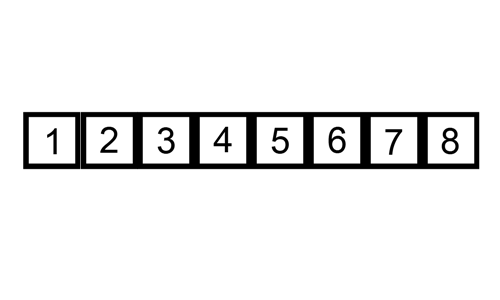
- 삽입으로 정렬 은 특정 데이터를 적절한 위치에 붙여넣습니다.
함께 삽입으로 정렬 특정 데이터가 올바른 위치에 놓이기 전에 데이터가 이 시점까지 이미 정렬되었다고 가정합니다.
정렬된 데이터 목록에서 일치하는 위치를 찾은 후 해당 위치에 삽입됩니다.
선택 정렬보다 구현하기 어렵지만 실행 시간 측면에서 선택 정렬에 비해 효율적인 알고리즘으로 알려져 있다.
붙여넣을 알고리즘 코드 정렬(Python)
# 삽입 정렬을 사용하여 오름차순 정렬
arr = (7, 5, 9, 0, 3, 1, 6, 2, 4, 8)
for i in range(1, len(arr)):
# 인덱스 i부터 1까지 감소하며 반복
for j in range(i, 0, -1):
# 인덱스 i부터 1까지 감소하며 반복하는 문법
# 이것을 사용한 이유는, 삽입 정렬의 경우 특정한 데이터의 왼쪽에 있는 데이터들은 이미 정렬이 된 상태이므로
# 자기보다 작은 데이터를 만났다면 더 이상 데이터를 살펴볼 필요가 없기 때문이다.
if arr(j) < arr(j - 1):
arr(j), arr(j - 1) = arr(j - 1), arr(j)
# 자기보다 작은 데이터를 만나면 그 위치에서 멈춤
else:
break
print(arr)
>>> (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)- 시간적 복잡성~이다 O(N^2)오전.
선택 정렬과 마찬가지로 이중 반복 때문에 O(N^2)입니다.
삽입으로 정렬 은 현재 목록에 있는 대부분의 데이터가 정렬되어 있으면 매우 빠릅니다. 최상의 경우 에)의 시간복잡도를 갖는다
※ 일반적으로 퀵소트와 비교 삽입으로 정렬 이 비효율적이지만 “거의 정렬된” 상황에서는 퀵 정렬 알고리즘보다 더 효율적입니다.
빠른 다양성
- 빠른 종류 은 기준 데이터(피벗) 조정 및 기준보다 큰 데이터와 작은 데이터 위치 변경 정렬 방법.
일반적인 상황에서 가장 일반적으로 사용되는 정렬 알고리즘 중 하나이며 병합 정렬과 함께 대부분의 프로그래밍 언어에서 정렬 라이브러리의 기반을 형성합니다.
가장 간단한 퀵 정렬에서는 첫 번째 데이터가 참조 데이터(피벗)로 설정됩니다.
퀵 정렬 알고리즘 코드(Python)
# 퀵 정렬을 사용하여 오름차순 정렬
arr = (7, 5, 9, 0, 3, 1, 6, 2, 4, 8)
def quick_sort(array, start, end):
if start >= end: # 원소가 1개인 경우 종료
return
pivot = start # 피벗은 첫 번째 원소
left = start + 1
right = end
while left <= right:
# 피벗보다 큰 데이터를 찾을 때까지 반복
while left <= end and array(left) <= array(pivot):
left = left + 1
# 피벗보다 작은 데이터를 찾을 때까지 반복
while right > start and array(right) >= array(pivot):
right = right - 1
if left > right: # 엇갈렸다면 작은 데이터와 피벗을 교체
array(right), array(pivot) = array(pivot), array(right)
else: # 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
array(left), array(right) = array(right), array(left)
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
quick_sort(array, start, right - 1)
quick_sort(array, right + 1, end)
quick_sort(arr, 0, len(arr) - 1)
print(arr)
>>> (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
Python을 활용한 Quicksort 알고리즘 코드
# Python의 장점을 살린 퀵 정렬
def quick_sort_better(array):
# 리스트가 하나 이하의 원소만을 담고 있다면 종료
if len(array) <= 1:
return array
pivot = array(0) # 피벗은 첫 번째 원소
tail = array(1:) # 피벗을 제외한 리스트
left_side = (x for x in tail if x <= pivot)
right_side = (x for x in tail if x > pivot)
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행하고, 전체 리스트를 반환
return quick_sort_better(left_side) + (pivot) + quick_sort_better(right_side)
print(quick_sort_better(arr))
>>> (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)- 시간 복잡도는 평균적인 경우입니다. O(NlogN)그리고 최악의 경우 O(N^2)의 시간복잡도를 갖는다
※ 데이터 개수가 많을수록 빠른 종류 위에서 설명한 선택 정렬 및 삽입 정렬보다 압도적으로 빠릅니다.
그러나 위의 코드와 같이 맨 왼쪽 데이터로 패닝하면 “데이터가 이미 정렬된 상태”일 때 느리게 작동합니다.
(이를 해결하려면 피벗 값을 설정할 때 별도의 로직을 추가해야 합니다. – 파이썬의 표준 정렬 라이브러리를 사용하여 O(NlogN) 보장)
| 데이터 수(N)/시간 복잡도 | O(N^2) (선택 정렬, 삽입 정렬) | O(NlogN)(퀵 정렬), 최악의 경우는 O(N^2) |
| N=1,000 | 약 1,000,000 | 약 10,000 |
| N=1,000,000 | 약 1,000,000,000,000(1조) | 약 20,000,000 |
위의 표는 데이터의 개수에 따라 얼마나 많은 작업이 필요한지를 보여주고 있으며 정확한 작업 수를 비교한 것은 아닙니다.
병합, 정렬

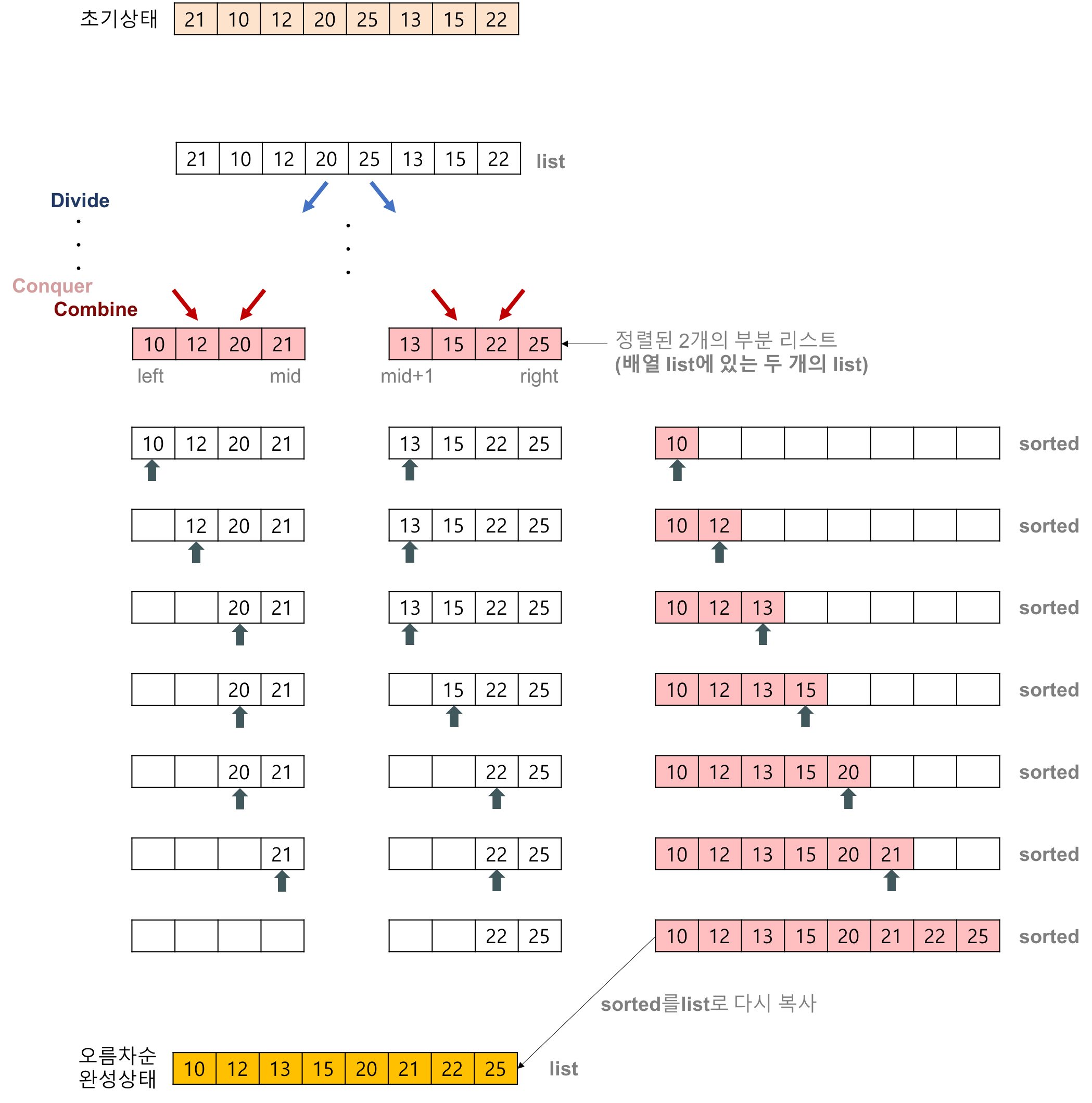
- 병합, 정렬 은 정렬되지 않은 모든 데이터를 하나의 단위로 나눈 후 분할된 데이터를 병합하여 정렬하는 방식입니다.
즉, 데이터를 공유합니다. 그런 다음 크기를 비교하고 정렬합니다(정복). 마지막으로 병합하십시오.
병합할 목록이 더 이상 없을 때까지 반복합니다.
병합 정렬 알고리즘 코드(Python)
# 병합 정렬을 사용하여 오름차순 정렬
arr = (7, 5, 9, 0, 3, 1, 6, 2, 4, 8)
def merge(left, right):
sorted_list = ()
i, j = 0, 0
while i < len(left) and j < len(right):
if left(i) <= right(j):
sorted_list.append(left(i))
i = i + 1
else:
sorted_list.append(right(j))
j = j + 1
# 남은 값들을 삽입한다.
while i < len(left):
sorted_list.append(left(i))
i = i + 1
while j < len(right):
sorted_list.append(right(j))
j = j + 1
return sorted_list
def merge_sort(array):
if len(array) <= 1:
return array
mid = len(array) // 2
left = merge_sort(array(:mid))
right = merge_sort(array(mid:))
return merge(left, right)
print(merge_sort(arr))
>>> (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
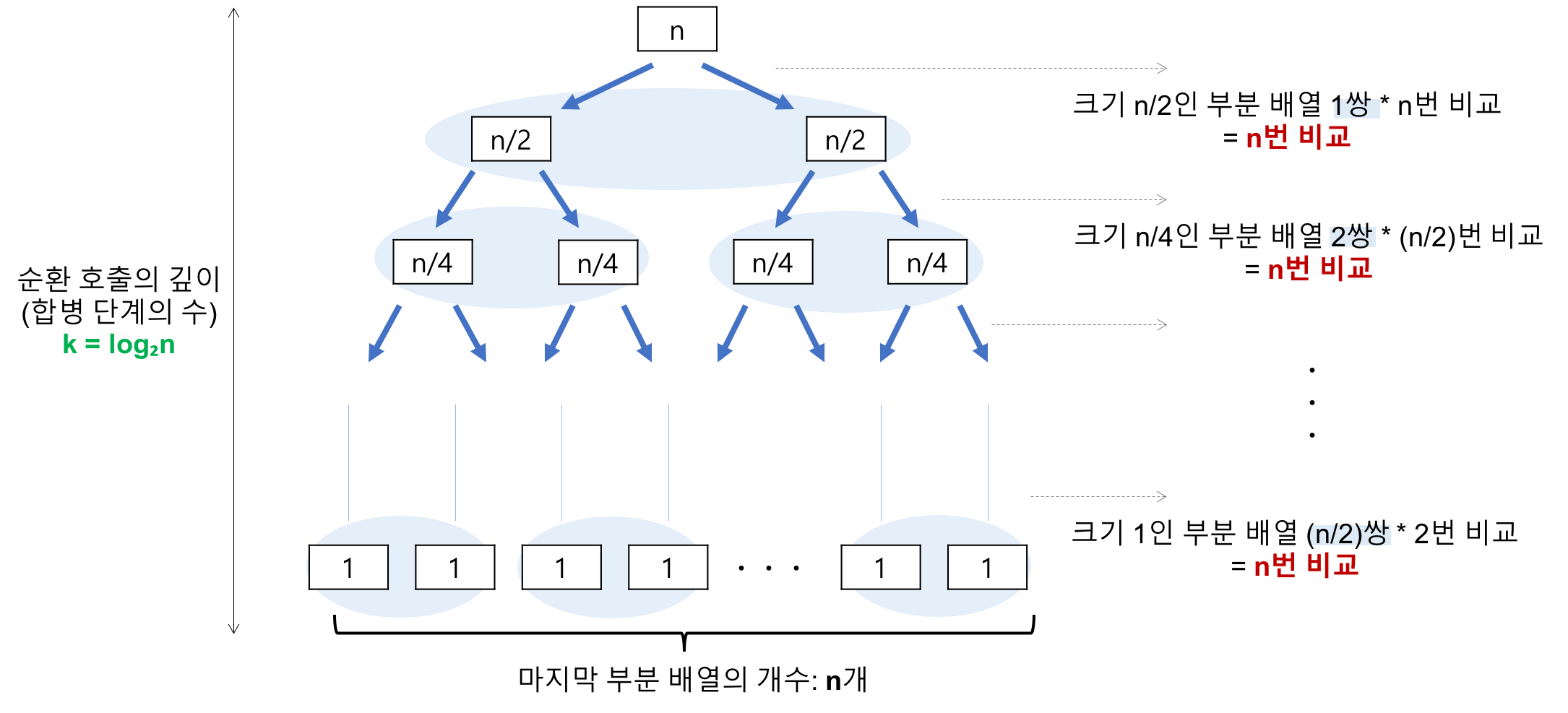
- 시간 복잡도는 O(NlogN)오전. (최악의 경우, 평균 및 최상의 경우의 시간 복잡도는 동일함)
크기가 N인 목록을 반으로 나눕니다. 한 번 분할 N/2 2개의 조각이 형성되고 나뉩니다. N/4 4개를 만듭니다.
이것을 반복하여 피날레 N/N 덩어리 N개가 나타난다
즉, 매번 분할 과정이 반으로 줄어들기 때문에 각 분할마다 병합 과정을 수행한다. O(NlogN)의 시간복잡도를 갖는다
정렬 카운팅
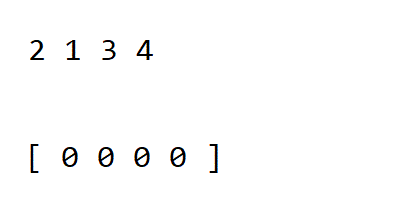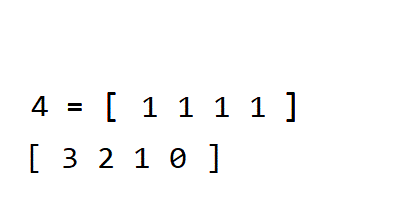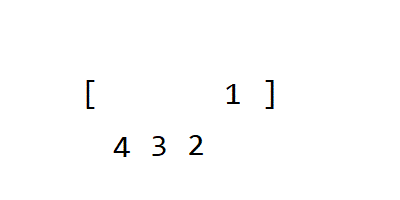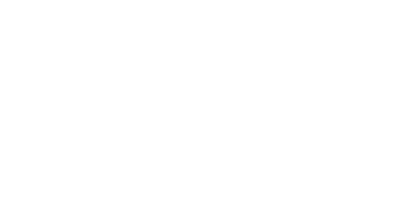
- 정렬 카운팅 은 특정 조건에서만 사용할 수 있지만 매우 빠르게 작동하는 정렬 알고리즘입니다.오전.
(여기에는 특별한 조건이 적용됩니다. 정렬 카운팅 데이터의 크기 범위가 제한적일 때 사용할 수 있으며 정수 형태로 표현할 수 있다.)
일반적으로 가장 큰 데이터와 가장 작은 데이터의 차이가 1,000,000을 넘지 않아야 효과적으로 사용할 수 있습니다.
정렬 카운팅 은 동일한 값으로 여러 날짜가 나타나는 경우에 유효합니다. 사용(예: 학생 성적, 차량 속도 데이터)
계수 정렬 알고리즘 코드(Python)
# 계수 정렬을 사용하여 오름차순 정렬
# 단, 리스트의 모든 원소의 값이 0보다 크거나 같다고 가정
arr = (7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2)
# 모든 범위를 포함하는 리스트 선언 (모든 값은 0으로 초기화)
count = (0) * (max(arr) + 1) # (0)이 array이 최대값만큼의 개수가 만들어져야 하므로 list index의 특성 +1을 해줌
for i in (arr):
# 데이터에 해당하는 인덱스의 값 증가
count(i) = count(i) + 1
# 리스트에 기록된 정렬 정보 확인
for i in range(len(count)):
for j in range(count(i)):
# 띄어쓰기를 구분으로 계수 정렬 이용한 오름차순 정렬
print(i, end = ' ')
>>> 0 0 1 1 2 2 3 4 5 5 6 7 8 9 9- 시간복잡도는 데이터의 개수가 N이고 데이터의 최대값(양수)이 K일 때 최악의 경우이다. 오(엔+케이) 보장하다
※ 계수 정렬은 때때로 심각한 비효율을 초래할 수 있습니다. 예를 들어 날짜가 0과 999,999 두 개뿐이라 하더라도 목록의 크기는 100만 개로 설정해야 합니다. 그것은 매우 비효율적입니다.
코딩 테스트의 정렬 알고리즘
- 정렬 라이브러리로 해결되는 문제: 표준 정렬 라이브러리를 사용하여 정렬 기술을 아는 것은 단순히 문제입니다.
- 정렬 알고리즘의 원리에 대한 질문: 문제를 풀기 위해서는 Selection Sort, Insertion Sort, Quick Sort, Merge Sort, Counting Sort의 원리를 알아야 합니다.
- 더 빠른 정렬이 필요한 문제: 퀵정렬 기반의 정렬 기법으로는 해결할 수 없지만, 카운트 정렬과 같은 다른 정렬 알고리즘을 사용하거나 문제에서 기존 알고리즘을 구조적으로 개선하여 해결할 수 있습니다.